Retângulo de Ouro ou Proporção Áurea

Rodrigo Pioto
Jun 30, 2015
3 min read

Resumo: Este artigo apresenta de forma simples a mágica existente por trás da razão de ouro e onde ela pode ser encontrada, além de explicar o porque essa razão é tão explorada nos trabalhos de marcenaria.

Introdução:

Figuras geométricas como Círculo, Quadrado, Triangulo e Retângulo estão mais que presentes na marcenaria. A maior parte dos cortes usam essas figuras por completo ou parte delas. Algumas são muito simples e não há muito segredo para traçá-las, por exemplo, um quadrado tem quatro lados iguais, um triângulo pode ser retângulo ou equilátero. Agora, e sobre o retângulo, qual seria o tamanho ideal dos lados?

Pergunta: qual a proporção ideal entre os lados?

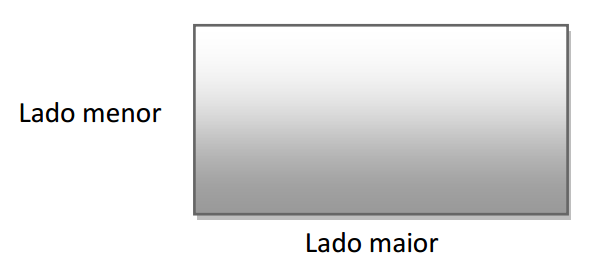
Existe um número resultante da razão (divisão) do “Lado maior” / ‘Lado menor” conhecido como Proporção Áurea ou número de ouro, que corresponde ao valor de 1,618 arredondado em três casas decimais.

Na natureza, como o corpo humano, plantas e animais essa proporção é presente e facilmente encontrada. Nas obras de arte e na arquitetura antiga e moderna também.

Retornando sobre a questão do retângulo, pode-se dizer que um Retângulo é de ouro quando a razão entre o Lado maior e o menor é de 1,618.

Isso não significa que se um retângulo não tiver exatamente essa proporção ele é imperfeito, mas para os olhos e também para o cérebro humano, sempre que essa proporção é capturada pelos sentidos, inconscientemente nota-se uma certa harmonia na peça. Isso significa que, se houver uma peça que apresente cortes, curvas e desenhos na razão de ouro, as pessoas de uma forma geral tendem a dizer que a peça está mais elaborada visualmente.

Em projetos de marcenaria essa razão também é aplicada com frequência. Existe um instrumento que mede a proporção áurea usado nas oficinas que é muito prático, pois não depende de uma calculadora para estimar os tamanhos do lado A e B. Basta articular esse tipo de “compasso” que automaticamente a razão de ouro é mantida.

Após comentar sobre a matemática que suporta essa razão, segue alguns exemplos um tanto curiosos sobre esse número ou razão.

Corpo Humano

A altura do corpo humano e a medida do umbigo até o chão.
A altura do crânio e a medida da mandíbula até o alto da cabeça.
A medida da cintura até a cabeça e o tamanho do tórax.
A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
O tamanho dos dedos e a medida da dobra central até a ponta.
A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.

Essas proporções anatômicas ideais foram representadas pelo "Homem Vitruviano", obra de Leonardo Da Vinci.

Arte

A razão de ouro também está presente numa das obras de arte mais famosas do mundo, Mona Lisa

As linhas vermelhas representam os eixos na vertical e horizontal. Note que os olhos e a boca estão situados na razão áurea (linha branca)

Arquitetura

Uma sequência de retângulos de ouro são facilmente encontrados arquitetura antiga e moderna. O Pantheon na Grécia mostra que a milhares de anos atrás essa razão já era conhecida.

A mesma sequência é encontrada na Catedral de Notre Dame na França.

A união dos arcos formados por uma sequência de retângulos dourados resulta numa espiral dourada. Essa espiral faz parte da estrutura orgânica de plantas, animais e outras formas na natureza.